
Musical Insights, Vol. 1 (Spring 1997) [Prev] [Next] [MACRO] [Journal Home] [Submissions]
Dominant-tonic progressions are considered the primary building blocks of music during the common practice period. As such, they command a substantial amount of theoretical study and analysis; nonetheless, only a limited amount of research has been devoted to the evolution of this phenomenon. Edward Lowinsky states that "the cadence is the cradle of tonality,"1 likewise the cadence is the origin of the circle series. A major concern is whether cadences found in music of the fifteenth century can be considered predecessors of the V-I, when composers of the period did not associate the cadence with a concept of verticality as presently understood. Yet historical perspective allows for the perception of germinal ideas in the fifteenth-century cadence that develop into the V-I progression found in the Baroque, Classical, and Romantic periods.
Certain contrapuntal practices facilitated the development of the common-practice authentic cadence as is presently understood. During the fifteenth century, every composition was to end with a perfect consonance, and this consonance was to be approached from the nearest imperfect interval. Contrary motion was highly emphasized, and the prohibition of parallel perfect intervals, not so important in the thirteenth and fourteenth centuries, became extremely significant.
Avoidance of parallel perfect intervals arises from one of two important elements that occurred in the fifteenth century. First, composers of the period often emphasized one axial pitch in a composition, forming a genesis of the present day tonal center. In order to maintain this axial pitch, parallel fifths had to be avoided. This is due to the fact that keys related by the interval of a perfect fifth inherently share six common pitches. Thus fifths can potentially reinforce more than one specific note.
Secondly, some composers wrote for four voices rather than the traditional three. Fifteenth-century rules dictate not only that a composition must end with a perfect consonance, but also that this perfect consonance must be approached by an imperfect consonance. For example, if a piece ended on a sonority based on C, the pitches used to approach this consonance should be B and D. If a third or fourth voice is added, the only choice that conforms to the restrictions imposed is the pitch G. These three pitches, whether present in a fifteenth- or nineteenth-century composition, can be combined to form what is known presently as a V chord in the key of C. Consequently, the incorporation of a fourth voice precluded any type of cadence other than the V-I similar to that found in the common practice period.
Another element that played a part in the development of the V-I cadential formula is the interval of a perfect fourth. In the thirteenth and fourteenth centuries, the perfect fourth was considered consonant, but by the fifteenth century it was deemed a dissonance. As a result, this causes a leap in the bass voice because the pitch G can only occur below the D, any other position would form a fourth above the bass. Thus, formation of the cadence became even more controlled.
As mentioned above, compositions were to end with a perfect consonance. All of the aforementioned rules were designed to develop an approach to this goal. If tonality is to be considered goal-directed motion, couldn't the approach and arrival of a perfect consonance be considered goal-directed motion of the fifteenth century? Hence, (1) the shift to four voices, (2) the increase in importance of the fifth and final, and (3) the prohibition of parallel fifths combine to form catalysts of the common practice cadence. The developmental process of these ideas is illustrated through excerpts chosen from nine composers practicing their art from 1400 through 1672. Whenever possible, the composers were chosen in order to trace trends from teacher to pupil, or at least between composers who reportedly had contact with one another. Four of the composers are included in this teacher to pupil relationship: Adrian Willaert, Andrea Gabrieli, Giovanni Gabrieli, and Heinrich Schütz. Guillaume Dufay, Johannes Ockeghem and Jacob Obrecht represent the second category, that of composers reportedly in contact with one another. Only two composers, Giovanni Palestrina and Jan Sweelinck, do not fit within either of these groups. They were chosen to fill historical gaps not covered by the other composers.
Even though the addition of a fourth voice provided much of the impetus for cadential development, seeds of this idea are found in three-voice works as well. In the following example, Alma redemptoris mater2 by Dufay (1400-1474), foreshadowings, not only of the V-I, but of the ii-V-I cadence as well. Figure 1.a illustrates an ancestor of the V-I cadence, and figures 1.b and 1.c illustrate predecessors of the ii-V-I, first moving to F and then to C.

Figure 1.a

Figure 1.b

Figure 1.c
Nonetheless, it is in the four-voice works of Dufay that most of the innovative aspects of fifteenth-century composition are observed. He, Compaignons, resvelons nous3 manifests a strong axial emphasis of the pitch G. Indeed, most of the composition is formed by shifts between G and its fifth, D. Since this work is in four voices, a greater variety of pitches are present at the cadences than those found in the three-voice works. For example, in measure two, all cadential pitches are present. A reductive analysis of measures 1-9 is included in figure 2 in order to illustrate the predominance of final and fifth, as well as relatively traditional cadences in this piece.



It becomes apparent from the reductive analysis in figure 2 that each contrapuntal line is woven around the fifth and final of the piece. The result is a vertical emphasis of these pitches as well, producing cadences such as those in measures 2, 4-5, and 8-9.
Similar cadences are present in the music of Ockeghem, (1425-1497), who composed during roughly the same period as Dufay. Several examples occur in the Kyrie from the Missa L'Homme Arme, in figure 3 [Davison and Apel, 1946, pp. 76-77]. As with He, Compaignons, resvelons nous, one axial pitch is highlighted, in this case G. However, the work does not emphasize the fifth and final as exhibited in the Dufay example. Notice the leap in the bass in each cadence. When the upper voices move primarily in conjunct motion, the bass requires the leap in order to satisfy fifteenth-century compositional requirements. Another interesting device employed in this work appears in figure 3.b with the Landini cadential material in the upper voice. The leap of a fourth found in figures 3.a, 3.b, and 3.c is applied in figure 3.d where the bass voice moves from D to F by fourths and then to B in the tenor voice of the next measure. Not all of these tones are chord roots, nonetheless the pattern foreshadows the bass motion found in many circle progressions today (see figure 3).

A true precursor of the circle series appears in the Tsaat een meskin by Jacob Obrecht, who lived from 1451-1505 [Davison and Apel, 1946, pp. 82-83]. This piece employs not only circle progressions, but multiple circle progressions in series as well. During the second half of the fifteenth century, a set of multiple circle progressions (henceforth referred to as circle series), is novel in and of itself. Not only did Obrecht extend the cadential formula from dominant-tonic to supertonic-dominant-tonic, but he employed a circle series as the foundation for a section of music in a manner rarely, if ever, seen before this time. In figures 4.a and 4.b, Obrecht utilizes the series D-G-C-F to form the structure for approximately three measures of music. Immediately following each of these two examples is another circle series, a dominant-tonic that has been extended into a subdominant-dominant-tonic on the pitches C, D, and G. This may be the first appearance of this cadential pattern; a pattern that would become prevalent in music of the common practice period.
One more circle series occurs in this piece at the same pitch level as the others, this time spanning seven measures (figure 4.c). The G in the series is prolonged and finally advances to C and F.

Figure 4.a

Figure 4.b and 4.c
Circle series were employed by other composers contemporary to Obrecht, among them Adrian Willaert, (1490-1562). In the fourth Ricercare of his IX Ricercari4, Willaert employs the pitches A-D-G and C, as seen in figure 5.a. It is possible to interpret this as a five note circle due to the short duration and passing nature of the Bb, illustrated in the following diagram.
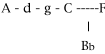

Figure 5.a

Figure 5.b
A five note circle series occurs in Willaert's Victimae paschali laudes [Davison and Apel, 1946, pp. 117-118] represented in the preceding figure 5.b. This circle series progresses from D to Bb in a span of two measures. As with the Obrecht examples, Willaert employs the circle series as more than a cadential formula, rather it becomes the foundation for this particular phrase.
Not only phrases, but at times entire works are based on circle progressions in the music of Andrea Gabrieli, (1510-1586), who studied under Adrian Willaert. For example, the entire eighteen measures of the Intonazione settino tono [Davison and Apel, 1946, pp. 146-147] are diagramed below. The score of the Intonazione settino tono follows in
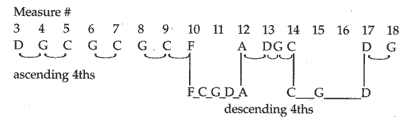

Figure 6.a.
In pieces of a more complicated nature, such as Ricercare del 12 tono [Davison and Apel, 1946, pp. 147-148], circle progressions appear as a sequence of simple cadences, extended cadences and circle series, (figure 6.b). Cadences like those found in measure 13-14 occur throughout the composition, and extended forms of the cadence, the supertonic-dominant-tonic, take place in measures 28-30, 49-51, and 52-54. In measures 49-51, a supertonic-dominant-tonic is followed by the same cadence type in augmentation.


Figure 6.b
Also observe that each time the supertonic occurs, it is in first inversion, a foreshadowing of one of the common cadential formulas of the Classical period, that of incorporating the fourth, fifth, and first scale degrees in the bass. This bass motion may also be an outgrowth of the root motion associated with voice-leading similar to the subdominant-dominant-tonic cadential formula of the eighteenth century, found as far back as Willaert's "Victimae paschali laudes" [Davison and Apel, 1946, pp. 117-118] in figure 6.c.

Figure 6.c
The only circle series in the composition appears in the form of an extended circle progression that occurs in measures 7-9 (Figure 6.b). All circles in this piece seem to fit into a coherent plan determined by Gabrieli at the beginning of the composition. For example, in measures 13-14 he presents only the circle progression G-C; later he extends this by one note back in the circle to D-G-C, forming the supertonic-dominant-tonic cadence, and finally, moves one note further back in the circle for the A-D-G-C employed in the circle series in measures 7-9. This is important in that the goal of every type of circle in the piece is the pitch C. Earlier it was stated that during the fifteenth-century composers emphasized one axial pitch; however, even with the development of the fifth and final, circle progressions emphasize several different pitches. For example, in the Victimae paschali laudes by Willaert, Andrea Gabrieli's teacher, there are circles that end on D, G, C, F, and one that proceeds to Bb. Interestingly enough, even though these pitches combined together form one large circle, A-D-G-C-F-Bb, Willaert does not employ these to attain one specific goal, but rather to emphasize different pitches within the piece. It is Andrea Gabrieli who first uses the circle progression to target a specific pitch, possibly touching on the concept of key and tonic.
Palestrina (1525-1594), employs circle progressions in the same manner as Gabrieli, presenting the original circle and then extending it. In figure 7.a, the circle moves from A through D to G; in figure 7.b, this circle is expanded to incorporate the C (second measure of the figure). Notice that the two circles are completed on different pitches unlike the example by Andrea Gabrieli. Just as Andrea Gabrieli expanded upon ideas found in Willaert, Gabrieli's developments are enhanced by his student and nephew Giovanni Gabrieli, who provides another link in this evolutionary chain.

Figure 7.a and 7.b
Many of the ideas previously mentioned appear in the music of Giovanni Gabrieli, among them the use of the circle series for prolongation, already seen in works of Obrecht. Gabrieli (1554-1612) obviously took the lessons of his uncle seriously, composing circles of greater length. The "Ricercari (5°)"5 from Gabrieli's organ compositions contains two extended full circle series. The novelty of these circles is that they incorporate not five-note circles, the largest seen thus far, but rather thirteen- and eleven-note circles within a two measure span (see figures 8.b and 8.c). Both series originate from the melodic use of thirds in the piece, occurring for the first time as seen in figure 8.a.
The extended full circle series in figure 8.b breaks when the melodic sequence of thirds is completed at the arrival of beat three in measure three. In the second series Gabrieli breaks the pattern, this time on beat three of the first measure (figure 8.c) in order to avoid the tritone formed by the Eb to A motion in the circle. Instead, he substitutes a first inversion C minor triad for the Eb. This practice of substitution becomes quite common in compositions of this era, and is occasionally employed in music of the common practice period as well.

Figure 8.a

Figure 8.b

Figure 8.c
Circle series in the music of Jan Sweelinck (1562-1621) may not be as lengthy as those of Giovanni Gabrieli, however, this is more than compensated for by prolific employment of smaller circles such as those present in Fantasia in echo [Davison and Apel, 1946, pp. 209-211].
Two types of circle series occur in this piece, those that proceed quickly occupying a short span of time--for example, one measure--and those that include a structural function of prolongation encompassing several measures or more. An example of the former is found in figures 9.a and 9.b. Note that three members of the series are contained within the span of one measure, and that each of the members, with the exception of the very first, have durations of one beat.

Figure 9.a and 9.b
However, in figure 9.c, the same circle series occurs, this time over five measures. Each pitch of the series incorporates the entire measure, except for the A that receives only two beats in the second measure. Actually, the fermata above the A would seem to compensate for its smaller durational value in comparison to the other pitches in the series.

Figure 9.c
The circle, E-A-D-G-C, is increased in length by one pitch in figure 9.d thus becoming E-A-D-G-C-F. Sweelinck treats this series in much the same manner as the aforementioned one in that it occurs in an expanded form later in the piece. In this particular occurrence of the circle, the E receives two beats, the A five, but the rest of the circle takes place within constraints of one beat per pitch.

Figure 9.d
Just as with the circle series in figure 9.c, the series is also expanded later in the piece, in figure 9.e. In this instance, the material on the pitch E again occurs within two beats, the A in four beats instead of five, D, G, and C are expanded to two beats each, and F is given one beat as before.

Figure 9.e
The final link, or culmination, of this evolutionary chain is provided by the music of Heinrich Schütz, (1585-1672), a pupil of Giovanni Gabrieli. The influence of Gabrieli is quite apparent, especially in the number of consecutive circle progressions that Schütz employs. Gabrieli's compositional style is also observed in Schütz's avoidance of the tritone. Both composers replace the chord root of the tritone with a chord root that is usually a third away from the replaced root. This phenomenon appears in music by Monteverdi as well, in works such as "Chi vuol verder" and "Godi pur del bel sen."
The following figure diagrams a set of circle progressions from the Ricercar (5°) by Gabrieli. Note not only the length of this progression, but also the characteristic omission of the tritone (figure 8.c, p. 22).
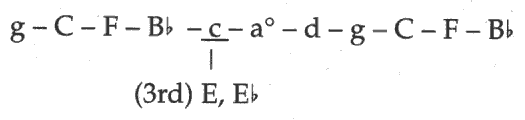
C is a third away from both pitches it could be substituted for; the E forms a tritone with the previous Bb, or the Eb that would form a tritone with the following A. Gabrieli concludes the circle on Bb, perhaps to avoid another encounter with a possible tritone.
Music by Schütz incorporates all of the aforementioned phenomenon, as well as new developments. In the first two staves of the "Allelujah" in the "Freuet euch des Herren ihr Gerechten" from the Symphoniae Sacrae (table 1), Schütz avoids the tritone by the same substitution method found in Gabrieli, in this instance replacing the Bb with the D a third away. However, in measure 142 Schütz does not avoid the tritone; this may be due to the following intrinsic difference between the patterns of circle progressions used by the two composers.
It appears that during the time of Gabrieli, the function of goal directed motion from circle progressions was not yet recognized, at least not to the extent found in Schütz. At times in the music of Gabrieli the tritone is circumvented, at others it is not (see table 1). This inconsistency, coupled with the fact that the circle progressions of Gabrieli do not come to rest on the tonic points to another function of this use of circle progressions. Circle progressions used by Schütz do tend to convey a feeling of arrival, a true sense of goal-directed motion. In the previously mentioned set of measures from the "Allelujah," Schütz appears to include the tritone the second time through the circle in order to establish a precursor of relative minor, and to prepare a strong arrival in this area at measure 143.
A lavish number of consecutive circle progressions are found in "Von Gott will Ich nicht lassen" by Schütz. Sixteen groups of circle progressions occur within the span of only 206 measures. Some of these extended progressions incorporate the tritone, while others make use of the third substitution previously mentioned. Each of the progressions in "Von Gott will Ich nicht lassen" targets the pitch G. At this point there can be little doubt that the circle progression is employed by the composer to facilitate goal-directed motion. Even though these circles have the same goal, they move toward this goal in different ways. Seven of the sixteen sets of circle progressions are interrupted; and in this case are completed, not by a substituted third, but by third inclusion. Some avoid the tritone by breaking the pattern completely at the point at which the tritone would occur. Examples are from "Von Gott will Ich nicht lassen" unless otherwise stated (table 1).
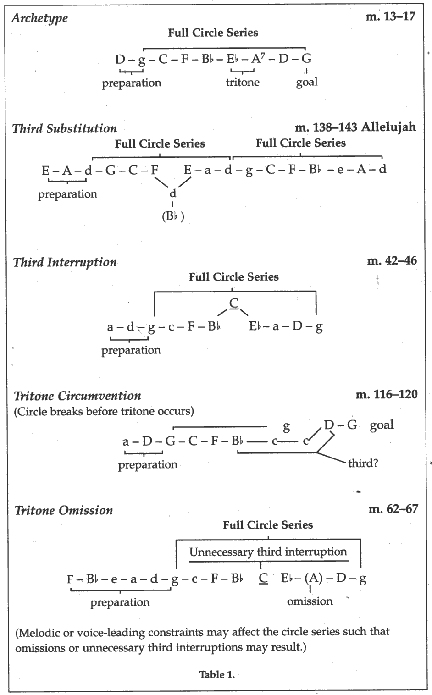
In studying music of these periods the evolutionary progression of the circle series becomes readily apparent. With such a profusion of this phenomenon in musical literature, it would follow logically that a coinciding abundance of theoretical discussion would also be available. However, this is not the case. Barring the customary circle of keys presented by many theorists, very little is mentioned regarding employment of circle series.
Possibly the earliest reference to the ascending fourth or descending fifth idea can be found in Musurgia Universalis6 by Athanasius Kircher (1601-1680). Here he refers to "circulationem harmonicam," or harmonic circles that are ascending and descending always by fourths or fifths, and that can be employed in such a manner as to end where one has begun. It seems that theorists after Kircher do not set aside a portion of their work for this idea. Instead, writers such as Heinichen, Mattheson, C. P. E. Bach, Kirnberger, and Rameau incorporate it into other aspects of theory in which it plays only a secondary role to the topic of discussion.
Two of the most famous circles are found in the works of Heinichen (1683-1729), and Mattheson (1681-1764). Figure 10.a represents the circle as developed by Heinichen in 1728, and 10.b represents the interpretation by Mattheson proposed in 1731.
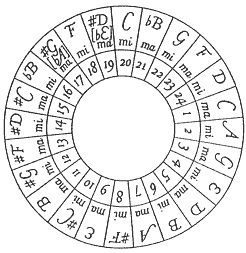

Heinichen developed his circle through discussions with Kuhnau concerning Kircher's method of demonstrating an orderly progression of keys by fourths or fifths. Since Kircher's method proved somewhat awkward by allowing a major key to proceed only to another major key, and a minor key to another minor key, Heinichen evolved his circle to permit more freedom.
Heinichen states that the composer may proceed through the circle in the following schemes:
(1) proceed through the entire circle of keys from either left to right, or right to left;
(2) move through alternate degrees of the circle of keys, either left to right, or right to left, starting with C major;
(3) same as above only starting with A minor.7
According to Heinichen, the musical circle is useful in composition, in accompanying from unfigured bass, in playing preludes on keyed instruments, and to facilitate the abolition of the ancient modes. Nonetheless, even though Heinichen considers the circle of keys to possess these many functions, he neglects to discuss any one of them in even cursory detail.
When Mattheson announced his circle of keys, he believed it to be an improvement on the circle by Heinichen. However, Mattheson is even more restrained in his treatment of the circle. The only significant difference between the two circles is that Mattheson simply requires one to traverse the circle in only one direction to get to any key, rather than both directions, as is necessary in the Heinichen design. Mattheson states his circle is an improvement on Heinichen's, and Heinichen declares Kircher as his source.
C. P. E. Bach presents a circle of keys in his Essay on the True Art of Playing Keyboard Instruments (1753-1762)8, but advocates modulation only to closely related keys, and again devotes minimal discussion to the employment of circles in composition. J. P. Kirnberger in The Art of Strict Musical Composition (1771-1779)9 presents the circle series as a chain of seventh chords intended to prevent repose (figure 11).
If one wants to keep the full cadence and yet prevent its effect of repose, the seventh need only be added to the tonic triad, whereby it becomes the dominant of a new key.10
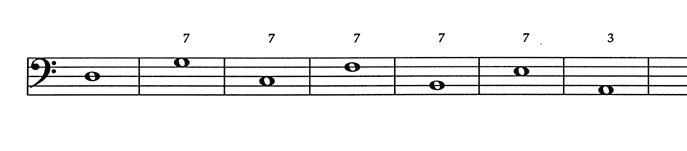
Figure 11.
This could conceivably work with any pattern in the bass, so why does Kirnberger choose a pattern of ascending fourths for this example?
This question may never be answered because, as mentioned previously, the ascending fourth pattern is presented only as a backdrop upon which to illustrate various theoretical constructs, in this case the function of the seventh.
Kirnberger then proceeds to discuss various correct methods of modulation, as does C. P. E. Bach. Kirnberger states that modulation should result only in movement to closely related keys, and that each of these keys should encompass at least one to two measures. This poses several interesting questions. If modulation through these keys is supposed to occur over one to two measure spans, one key at a time, how is this reconciled with the music of J. S. Bach in which one can find many instances of full circle series occurring twice over the span of two measures? Is it possible that the term "key" has a different meaning in this particular context? Or is it possible that at this point in history only the linear aspects of the circle series were noted, and thus the harmonic elements of the circle series were not considered as modulatory key relations?
Few answers to these questions can be found in the theoretical works of Rameau. Rameau discusses a fundamental bass that can proceed by consonant intervals of a third, fourth, fifth, or sixth, each of which can either ascend or descend. The only other statement of importance made in reference to the fundamental bass is that the smaller intervals are preferred over the large. Using the smaller intervals for the fundamental bass would include the third, but whenever Rameau refers to the fundamental bass in his examples, it always progresses by fourths. All of the following examples in figure 12.a-12.d are from Rameau's Traite de L'Harmonie (1722).11
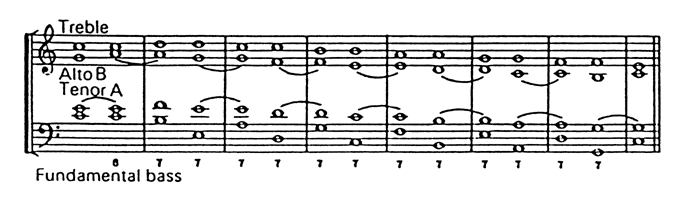
Figure 12.a
In figure 12.a one finds almost two full circle series. If Rameau had included the F in the second half of the first measure both circles would be complete. In example 12.b, Rameau again illustrates the fundamental bass as a progression of alternating descending fifths and ascending fourths, this time including two complete full circle series. Figures 12.c and 12.d represent the fundamental bass as a progression of ascending fourths and fifths as well. It is also interesting to observe that each time Rameau presents a fundamental bass in fourths, every chord, with the exception of the final one, incorporates the seventh as
a necessary chord element employed to avoid a cadence. In fact, in figure 12.c, Rameau includes the fundamental bass as a foundation upon which he can show the preparation and resolution of sevenths and
seconds, and in figure 12.d, refers to the fundamental bass as a "fundamental bass of sevenths." As with those authors previously discussed, the circle series aspects of the Rameau examples are not defined because of their secondary nature to the subject at hand.

Figure 12.b
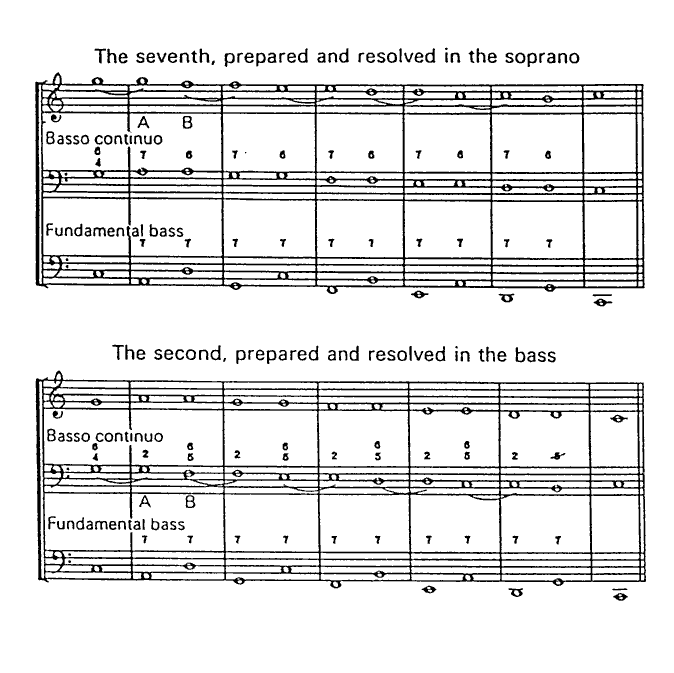
Figure 12.c

Figure 12.d
Some interesting questions arise from the previous illustrations. Does Rameau really consider the seventh a requirement for this particular form of the fundamental bass, or was it conceivable to have a fundamental bass without sevenths? Why does Rameau present so many examples of the fundamental bass in which the interval of a fourth is employed, when he considers the third, fifth, and sixth perfectly suitable consonances to apply as the fundamental bass?
Only one theorist appears to have discussed the circle series based upon its actual behavior in musical literature, especially in regards to the prolongational element seen in compositions as early as Obrecht. In his Die Grundsätze der musikalischen Komposition (1853-4)12 , Sechter treats the circle series, not as an abstract theoretical entity, but rather as a valid theoretical construct with specific, varied functions in music. Voice-leading, seventh and ninth chords, major and minor, and diatonic and chromatic structures or variations of the circle series are analyzed in depth. The following figures are presented with text translated from the original German by the author.
This order has its good points, in that the fifth of each following chord is prepared, as the octave of the proceeding chord becomes the fifth (referring to figure 13.a).

When employing I-IV-V-I one can insert a II chord in between in various manners as follows:
I-IV-II-V-I or I-IV-II-V7-I or I-IV-II7-V7-I. One can then substitute a VI chord for the IV chord.
I-VI-II7-V-I or I-VI7-II-V7-I or I-VI-II7-V7-I
To lengthen the statement, proceed the VI with a III.
I-III-VI-II-V-I or I-III-VI-IV-II7-V-I or I-V-III-VI-II-V-I
In order to extend the statement even farther, one follows the chord of the fourth with the seventh, the third follows, and so on as seen below.
I-IV-VII-III-VI-II-V-I or I-IV-VII7-III7-VI7-II7-V7-I
All of these sentences can be formed with root position chords, or with their inversions. Incorporating seventh chords into the statement prolongs restlessness that is only resolved in the chord of the first step.
Figure 13.b
Sechter also discusses the circle series in terms of goal-directed motion, specifically citing various capabilities in regards to modulation, thus expanding upon the germinal ideas of Heinichen and Mattheson. In figure 13.c, Sechter illustrates the method by which one can modulate from G major to A minor through employment of the circle series.
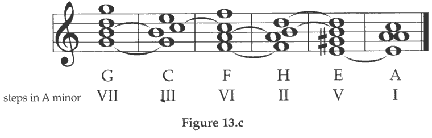
The example in figure 13.d illustrates Sechter's concept of prolongation within the circle series, an idea that has appeared in music since Obrecht, but nonetheless overlooked by most theorists before and after Sechter. The concept of prolongation within the circle series implies a hierarchy, similar to that found in Schenker, in which each member of the circle series maintains its status until the following member of the series is sounded, regardless of what material occurs in between.
If chords related by a leap of a fourth or fifth are interrupted by other material, only the two fundamentals are valid, as follows.

Sechter practices his theory within his compositional style. The following discussion is based on a page of the "Pastoral-Fuge" from the Drei Fugen.13 Elements of goal-directed motion, modulation and prolongation are all present here (see figure 14).
The first goal at the top of the page is the pitch D that is prolonged for three measures until the C natural appears to set the stage for the next arrival on G in measure 21. The G is then sustained until the C# and D# in measure 23, in conjunction with the B major triad, break the circle and begin a new one that first rests on E in measure 24. The full circle is completed in measures 25-26, however it is then continued so that the arrival of D, the tonic of the piece, coincides with the statement of the fugal theme. Patterns such as these occur throughout the composition, as well as in other Sechter works.

Figure 14.
Two things become evident from the previous series of analyses. The first is that, with the exception of Sechter, the most accurate portrait of the circle series is to be gleaned only through study of the actual music; and second, if the profusion of circle series within this music is to be considered an indication, there exists an abundance of prospective theoretical analysis. This is by no means an exhaustive or definitive study on the subject, but rather a catalyst that hopefully facilitates further research and imput on this topic by other individuals.
1.a Davison, Archibald T, and Apel, Willi, Historical Anthology of Music. Cambridge, Mass.: Harvard University Press, 1946, p. 70, mm. 39-44.
1.b Davison and Apel, p. 70, mm. 20-23.
1.c Davison and Apel, p. 70, mm. 25-28.
2. Author
3. Davison and Apel, p. 77, m. 8-41.
4.a Davison and Apel, p. 82, mm. 8-12.
4.b Davison and Apel, p. 83, mm. 27-38.
4.c Davison and Apel, p. 83, mm. 27-38.
5.a Willaert, Adrian, IX ricercari per sonar con tre stromenti. London: Schott and Co. Ltd., New York: Associated Music Publishers, 1933, mm. 94-99.
5.b Davison and Apel, pp. 117-118, mm. 58-60.
6.a Davison and Apel, pp. 146-147.
6.b Davison and Apel, pp. 147-148.
6.c Davison and Apel, p. 117, mm. 41-47.
7.a Palestrina, Giovanni, Ricercari sopra li tuoni a quattro. New York: Schott Music Corp. (Associated Music Publishers Inc.), 1933, pp. 18-19, m. 14.
7.b Palestrina, pp. 18-19, mm. 24-25.
8.a Gabrieli, Giovanni, Composizioni, Vol. II. Italy: G. Ricordi and C. Milano, 1958, pp. 18-21, mm. 4-5.
8.b Gabrieli, Giovanni, pp. 18-21, mm. 44-46.
8.c Gabrieli, Giovanni, pp. 18-21, mm. 74-75.
9.a Davison and Apel, pp. 209-211, mm. 5-6.
9.b Davison and Apel, pp. 209-211, mm. 9-10.
9.c Davison and Apel, pp. 209-211, mm. 24-28.
9.d Davison and Apel, pp. 209-210, mm. 10-13.
9.e Davison and Apel, pp. 209-211, mm. 87-91.
10.a Arnold, F. T., The Art of Accompaniment from a Thorough-Bass. London: The Holland Press, 1961, p. 267.
10.b Arnold, F. T., p. 276.
11. Kirnberger, J. P., The Art of Strict Musical Composition. Yale University Press, 1982, p. 117.
12.a Rameau, Jean-Phillipe, Treatise on Harmony. Trans and ed. by Philip Gossett, New York: Dover Publications, Inc., 1971, p. 255.
12.b Rameau Jean-Phillipe, p. 257.
12.c Rameau, Jean-Phillipe, p. 261.
12.d Rameau, Jean-Phillipe, p. 305.
13.a Sechter, Simon, Die Grundsätze der musikalischen Komposition. Leipzig: Breitkopf and Härtel, 1853-1854, p. 13.
13.b Sechter, Simon, p. 102.
13.c Sechter, Simon, p. 105.
13.d Sechter, Simon, p. 21, p. 95, p. 199 (author's transcription).
14. Sechter, Simon, Drei Fugen. Wein, Munchen: Ludwig Doblinger (Bernhard Herzmansky) K.G., 1972, pp. 2-5, mm. 16-32.